自信息
自信息(self-information)表示一个事件发生所蕴含的信息量,定义如下
\[ \mathrm{I}_{X}(x)=-\log \left[p_{X}(x)\right]=\log\frac{1}{p_{X}(x)} \]
自信息有三条性质
- 一个事件以概率1发生,则信息量为0
- 事件发生概率越小,所含信息量越多
- 两个独立事件同时发生,信息量应为两个自信息之和
满足这三条性质的只有上面这个公式(常数项系数省略),因此有上面的定义。其中\(\log\)的底数通常取\(2\),使用\(e\)或\(10\)也可以。
理解:比如2016年美国大选,大家原本预计希拉里赢面更大。如果最后希拉里赢了,我们会认为没什么信息量,大家都知道的事情;但如果最后特朗普赢了,我们会很吃惊,这就包含了更大的信息量。
信息熵的定义
随机变量的熵是自信息的期望值。当随机变量\(X\)离散时,熵(Entropy)定义如下
\[ H(X)=E_x \left[\log \frac{1}{p_{X}(x)}\right] = \sum_{x\in \mathrm{support}(X)} p_{X}(x)\log \frac{1}{p_{X}(x)} \]
熵\(H(X)\)的特点
- 熵衡量的是随机变量的不确定性、混乱程度;或者说为消除不确定性所需要的统计信息量
- \(H(X)\geq 0\)
- 当\(X\)只能取一个值时,概率为1,此时\(H(X)=0\)。表示没有不确定性,熵最小
- 当\(X\)在所有(\(n\)个)取值上概率相等时,熵最大,因为所有事件都有可能发生,不确定性最大。此时熵值为\(\log n\)
注意:个人不认为熵能衡量随机变量所蕴含的信息量,即使它是信息量的期望,因为这种认识比较违背直观。对比:(1)三个事件概率为\((\frac13, \frac13, \frac13)\);(2)三个事件概率为\((\frac23, \frac19, \frac29)\)。感觉第二个蕴含的信息量更多,因为比如有人告诉你三个事件等可能,就和没说一样,没包含什么信息量;而第二种你就知道哪个事件更可能发生,因此第二种包含了更大的信息量。
联合熵和条件熵
两个随机变量的联合熵(Joint entropy)定义如下
\[ H(X, Y)=\sum_{x, y} p(x, y)\log \frac{1}{p(x, y)} \]
条件熵(Conditional entropy)定义如下
\[ H(Y|X)=E_x [H(Y|X=x)]= \sum_{x, y} p(x, y)\log \frac{1}{p(y|x)} \]
注意:条件熵的结果不依赖\(X\)取值,是\(\sum_{y} p(y|x)\log \frac{1}{p(y|x)}\)又对\(X\)取了期望的结果。这个条件熵表示知道\(X\)后\(Y\)的不确定性,推导如下
\[ \begin{aligned} H(Y|X)&=E_x [H(Y|X=x)]\\ &=\sum_{x} p(x) \sum_{y} p(y|x)\log \frac{1}{p(y|x)}\\ &=\sum_{x} \sum_{y} p(x)p(y|x)\log \frac{1}{p(y|x)}\\ &=\sum_{x, y} p(x, y)\log \frac{1}{p(y|x)} \end{aligned} \]
下面给出一些性质
1、当\(X\)与\(Y\)独立时有
\[ H(Y|X)=H(Y) \]
\[ H(X, Y)=H(X)+H(Y) \]
2、一般情形下有
\[ H(X, Y)=H(X)+H(Y|X) \]
3、更一般地有(Chain rule)
\[ H(X, Y, Z)=H(X)+H(Y|X)+H(Z|X, Y) \]
\[ H(X_1, X_2, \ldots, X_n)=H(X_1)+H(X_2|X_1)+\ldots +H(X_n |X_1, \ldots, X_{n-1}) \]
顺序都不影响,比如
\[ H(X, Y)=H(X)+H(Y|X)=H(Y)+H(X|Y) \]
证明过程都类似下面这样
\[ H(X, Y)=\sum_{x, y} p(x) p(y)\left(\log \frac{1}{p(x)}+\log \frac{1}{p(y)}\right)=H(X)+H(Y) \]
4、一般情形下有
\[ H(Y|X)\leq H(Y) \]
\[ H(X, Y)\leq H(X)+H(Y) \]
\[ H(X_1, \ldots, X_n)\leq \sum_{i=1}^n H(X_i) \]
直观理解第一个式子:知道\(X\)的信息可以降低\(Y\)的不确定性(\(X\)与\(Y\)不独立时)。第二个式子把\(H(X)\)移项过去,和第一个式子是一样的。证明如下
\[ \begin{aligned} &H(X, Y)- H(X)-H(Y) \\ =&\sum_{x, y} p(x, y)\log \frac{1}{p(x, y)}- \sum_{x} p(x)\log \frac{1}{p(x)}- \sum_{y} p(y)\log \frac{1}{p(y)} \\ =&\sum_{x, y} p(x, y)\log \frac{1}{p(x, y)}- \sum_{x,y} p(x,y)\log \frac{1}{p(x)}- \sum_{x,y} p(x,y)\log \frac{1}{p(y)} \\ =&\sum_{x, y} p(x, y)\log \frac{p(x)p(y)}{p(x, y)} \\ \leq& \log \sum_{x, y} p(x, y)\frac{p(x)p(y)}{p(x, y)} \qquad \text{by Jensen’s Inequality}\\ =&\log 1 = 0 \end{aligned} \]
互信息
随机变量\(X\)和\(Y\)的互信息(Mutual information)定义如下
\[ \begin{aligned} I(X ; Y)&=H(X)-H(X | Y) \\ &= H(X)+H(Y)-H(X, Y)\\ &=H(Y)-H(Y|X) \\ &= I(X; Y)\\ &=\sum_{x, y} p(x, y)\log \frac{p(x, y)}{p(x)p(y)} \end{aligned} \]
互信息表示两个随机变量,知道其中一个,对另一个的不确定性降低程度。
根据上一节可知
- \(I(X;Y)\geq 0\)
- 当\(X\)与\(Y\)独立时,\(I(X;Y)= 0\)
各种熵的关系如下所示
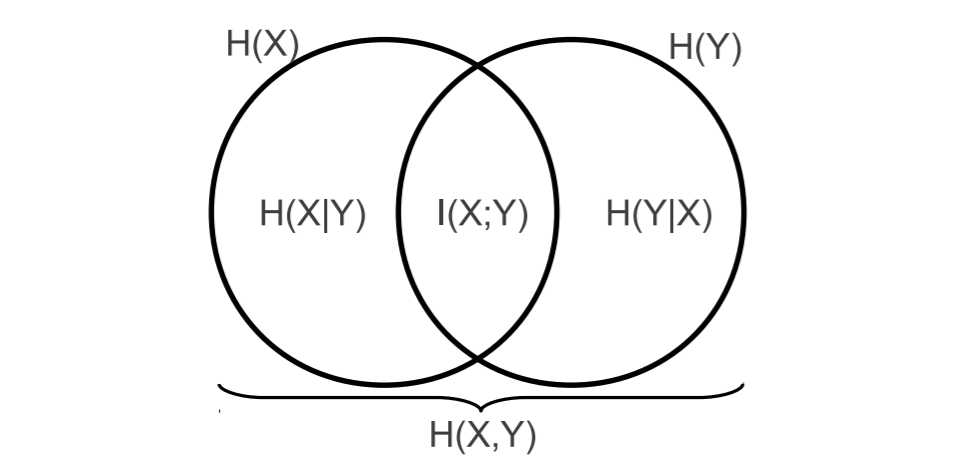
条件互信息(Conditional mutual information)定义如下
\[ \begin{aligned} I(X; Y | Z) &=H(X | Z)-H(X | Y, Z) \\ &=H(Y | Z)-H(Y | X, Z) \end{aligned} \]
KL散度
KL散度(KL-divergence)别名:相对熵(relative entropy)、信息散度(information divergence),用于衡量两个分布的差异,定义如下
\[ D(p \| q)=\sum_{x \in U} p(x) \log \frac{p(x)}{q(x)} \]
KL散度有如下性质
- 不对称性,\(D(p \| q)\neq D(q \| p)\)
- 只有当\(q\)的定义域(非0区域)包括\(p\)时,KL散度才不是无穷
- \(D(p \| q)\neq D(q \| p)\geq 0\),当\(p=q\)时取到0
- 互信息是在衡量\(p(x, y)\)与\(p(x)p(y)\)的KL散度
- \(I(X ; Y)=D(p(x, y) \| p(x) p(y))\)
第三条性质证明如下
\[ \begin{aligned} -D(p \| q)&=\sum_{x} p(x) \log \frac{q(x)}{p(x)}\\ &\leq \log \sum_{x} p(x) \frac{q(x)}{p(x)} \qquad \text{by Jensen’s Inequality}\\ &= \log 1 = 0 \end{aligned} \]
其中Jensen不等式取等号的条件是\(\frac{q(x)}{p(x)}\)为常数。
交叉熵
两个分布\(p\)和\(q\)的交叉熵(Cross entropy)定义如下
\[ H_{\mathrm{cross}}(p, q) = \sum_x p(x)\log \frac{1}{q(x)} \]
在分类问题中,用交叉熵做损失函数,此时\(p(x)\)表示数据的真实分布,\(q(x)\)表示模型估计出的分布。可以通过KL散度来理解这个式子
\[ \begin{aligned} D(p \| q)&=\sum_{x} p(x) \log \frac{p(x)}{q(x)}\\ &= \sum_{x} p(x) \log \frac{1}{q(x)}- \sum_{x} p(x) \log \frac{1}{p(x)}\\ &= H_{\mathrm{cross}}(p, q)-H(p) \end{aligned} \]
\(p(x)\)对应已知的数据,则第二项是个常数,因此最小化交叉熵相当于最小化这个KL散度,也就是让模型的估计分布更接近数据的真实分布。
从上面的推导也可以看出,交叉熵大于等于信息熵。
另外,也可以用编码角度理解熵、交叉熵、KL散度:知乎:如何通俗的解释交叉熵与相对熵?
参考资料
- 各种熵的定义和关系参考课件
- KL散度参考课件
- 博客:机器学习中各种熵的定义及理解