MCMC采样算法

介绍MCMC采样算法的中文博客中，LDA数学八卦-3：MCMC 和 Gibbs Sampling堪称经典，这篇文章包括它的转载引用，相信引导了无数读者入门，包括我自己在内。但此文并非完美，文中有一处错误困扰我很久，对算法设计的动机方面也没有详细说明，本人经过查阅思考总结出这篇文章，算是对上面博客的补充，希望读者阅读之前先对上面文章内容有所了解，本文将不会对基础概念多加说明。下面如果提到这篇博客，将称之为“引用博客”。

本文主要内容包括

  • 对MCMC采样算法思想的简单总结
  • 对引用博客中的错误加以说明，并渗透性地对引用博客的说法进行补充
  • 从算法设计者的角度出发来理解这些算法
  • 开脑洞，做实验，解决疑惑

基本介绍

马尔科夫链采样

要生成服从目标分布的样本，如果知道它对应的状态转移矩阵，可以利用这个矩阵完成：随机确定一个初始值，根据状态转移矩阵随机转移，每次转移的结果记录下来，得到一组样本，从一个阈值往后截取，这部分样本就会服从目标分布。

由马氏链定理可知，一个状态转移矩阵多次转移可以收敛于一个特定分布；所以对任意初始点，经过足够多次转移后的每个状态，都会服从这个特定分布；因此这个过程截掉前半部分没有收敛时的样本，留下的就是服从这个分布的样本。

上面的过程中，我们已知状态转移矩阵\(P\)，通过\(P\)的乘方可以计算出，通过这个状态转移矩阵生成的样本是服从什么样的分布。但是现实的问题往往是反过来，已知一个分布，要获得服从该分布的样本，我们如何找到这样一个\(P\)进行转移。

细致平稳条件

我们可以通过细致平稳条件来找这个\(P\)。

细致平稳条件是说：如果非周期马氏链的转移矩阵\(P\)和分布\(\pi(x)\) 满足

\[ \pi(i) P_{i j}=\pi(j) P_{j i} \quad \text { for all } i, j \]

则\(\pi(x)\)是马氏链的平稳分布。这是平稳分布的充分条件而非必要条件，即这是一个更强的条件。直观理解如下

  • 平稳分布指对任意一个状态，从这个状态转移出去的概率质量等于转移进来的概率质量，所以\(\pi(x)\)经过\(P\)转移后，每个状态的概率都没有变。
  • 细致平稳条件指对任意两个状态\(i\)和\(j\)，每一次转移\(i\)转移给\(j\)的概率质量等于\(j\)转移给\(i\)的概率质量；因此细致平稳条件更细节，它满足则平稳分布一定满足。

证明：我们想证满足细致平稳条件的\(\pi\)，可以使\(\pi P=\pi\)成立（因为满足这个式子的\(\pi\)是唯一的，所以只要这个式子成立就是平稳分布）；只需要证对每个\(j\)，都有

\[ \sum_{i=1}^{\infty} \pi(i) P_{i j}=\pi(j) \]

成立。证明如下

\[ \sum_{i=1}^{\infty} \pi(i) P_{i j}=\sum_{i=1}^{\infty} \pi(j) P_{j i}=\pi(j) \sum_{i=1}^{\infty} P_{j i}=\pi(j) \tag{1} \]

现在，回到找\(P\)的问题上来，我们原来是要找到一个\(P\)，满足\(\pi\)是这个\(P\)对应马氏链的平稳分布；现在我们只需要找到一个\(P\)满足细致平稳条件。

MCMC采样算法

我们要找一个\(P\)满足这个公式

\[ \pi(i) P_{i j}=\pi(j) P_{j i} \quad \text { for all } \quad i, j \]

先随便找一个转移矩阵\(Q\)，一般\(Q\)不满足细致平稳条件，即

\[ \pi(i) Q_{ij} \neq \pi(j) Q_{ji} \]

但我们可以乘一个数令它满足，令\(\alpha_{ij}=\pi(j) Q_{ji}\)，则

\[ \pi(i) Q_{ij} \alpha_{ij} = \pi(i) Q_{ij}\pi(j) Q_{ji}= \pi(j) Q_{ji}\pi(i) Q_{ij}=\pi(j) Q_{ji} \alpha_{ji} \]

令\(Q'_ {ij} = Q_{ij} \alpha_{ij}\)，则满足

\[ \pi(i) Q'_ {ij} = \pi(j) Q'_{ji} \]

但是要注意，\(Q'\)仍然不是我们要找的\(P\)，因为它不是一个概率转移矩阵，它的每一行加起来不是1，也更谈不上它满足细致平稳条件。如果用这个矩阵去转移，最后不会收敛到一个分布（乘方趋于0）。而且MCMC算法也不是这样做的。

这里我们也把MCMC算法的截图放上来

算法中不是将\(Q'\)当做一个整体来看待，而是拆分成转移概率\(Q\)和接受率\(\alpha\)，假设从\(i\)转移到\(j\)的过程中

  • 从\(Q\)中选到状态\(j\)，同时还被接受了，才真正完成转移，概率其实就等于\(Q_{ij}\alpha_{ij}=Q'_{ij}\)
  • 如果没被接受，则相当于转移到了\(i\)自身
  • 可以看到，算法中从\(i\)转移到\(\forall j\neq i\)时，是按照\(Q'_ {ij}\)的概率；但从\(i\)转移到\(i\)时的概率不止是\(Q'_{ij}\)的概率，而且加上了剩余的所有概率（因为\(Q'\)每一行加起来不足1）

因此我们要找的\(P\)就浮出水面了，即把\(Q'\)每一行不足1的那部分概率全加到对角线上，得到的新矩阵\(Q^*\)就是我们要找的\(P\)。

MCMC算法的过程，就等价于拿这个\(Q^*\)直接转移。

这样做确实满足每一行概率和是1了，但是它是否仍然满足细致平稳条件呢？

仍然满足！

  • 对于\(i\neq j\)的情形，数字没有变化，因此公式依然成立
  • 对\(i=j\)的情形，对角线数值改变，等式两边会同时改变，所以式子依然成立

因此\(Q^*\)就是我们要找的转移矩阵。

补充说明

  • \(Q'\)不是转移矩阵这一点就是引用博客以及几乎所有中文博客的误区。
  • 我们说\(Q'\)不是转移矩阵，但它仍满足细致平稳条件的那个公式，会不会从这个公式依然可以推出平稳分布呢（关注式子\((1)\)）？不会。看式子\((1)\)的最后一步，因为\(P\)加和不是1，所以最后一步不成立。
  • 看过引用博客的读者可能会有这样的疑问：为什么在被\(\alpha\)拒绝之后要令\(X_{t+1}=x_t\)，而不是忽视此轮重新抽样？希望能从\(Q^*\)的构造中得到解答。
  • 我们虽然能理解为什么\(X_{t+1}=x_t\)，但“忽视此轮重新抽样”的方式真的不能达到目标吗？不能。因为这相当于将停留在原地的很多样本去掉，虽然样本停留在原地这种情况在每一个状态中都会发生，但量不一样，这就要看\(Q'\)每行不足1的概率大小了。这一点会在下一节的最后一部分代码中得到检验。
  • 按照构造\(Q^*\)的思路，剩余的概率只有加到对角线上才行吗？是的，如果加到其他位置将违反细致平稳条件。
  • 为什么MCMC算法要有接受率\(\alpha\)这个说法，直接说\(Q^*\)不就好了？因为后者只是在这个例子中有效，这一点会在后文详细说明。

MCMC采样算法实现

下面我们用一个简单的例子验证上述的说法，使用R语言

\(Q'\)说明

1
2
3
4
5
6
7
8
9
10
11
12
13
library(expm) # 矩阵乘方 %^%

# 目标分布
p <- c(0.6, 0.3, 0.1)
# 随便取一个Q
q <- matrix(c(0.5, 0.3, 0.2,
              0.25, 0.05, 0.7,
              0.1, 0.8, 0.1), ncol=3, byrow=T)
# 计算alpha
alpha <- t(p * q)

# 计算Q'
q1 <- alpha * q

输出结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
> alpha
     [,1]  [,2] [,3]
[1,] 0.30 0.075 0.01
[2,] 0.18 0.015 0.08
[3,] 0.12 0.210 0.01
> q1
      [,1]    [,2]  [,3]
[1,] 0.150 0.02250 0.002
[2,] 0.045 0.00075 0.056
[3,] 0.012 0.16800 0.001
> q1 %^% 5
             [,1]         [,2]         [,3]
[1,] 9.582256e-05 2.228407e-05 8.383348e-06
[2,] 4.456814e-05 8.422126e-06 8.169187e-06
[3,] 5.030009e-05 2.450756e-05 3.313696e-06

可以看到，\(Q'\)每一行加总不足1，用\(Q'\)来转移，概率会越来越小。

\(Q^*\)说明

1
2
3
4
5
6
7
8
9
10
11
# 将剩余的概率加到对角线上
add_diag <- function(q){
  diag(q) <- diag(q) + (1 - apply(q, 1, sum))
  q
}

# 计算Q'
q1 <- alpha * q

# 计算Q*
q2 <- add_diag(q1)

输出结果

1
2
3
4
5
6
7
8
9
10
> q2
       [,1]   [,2]  [,3]
[1,] 0.9755 0.0225 0.002
[2,] 0.0450 0.8990 0.056
[3,] 0.0120 0.1680 0.820
> q2 %^% 100
          [,1]      [,2]       [,3]
[1,] 0.6008666 0.2993984 0.09973499
[2,] 0.5987967 0.3008353 0.10036795
[3,] 0.5984099 0.3011038 0.10048623

可以看到，\(Q^*\)迭代多次可以趋近于目标分布\(\pi\)

MCMC算法采样

这里我们用标准的MCMC算法进行采样，使用转移矩阵\(Q\)生成目标分布\(\pi\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 目标分布pi
p <- c(0.6, 0.3, 0.1)

# 随便取一个Q
q <- matrix(c(0.5, 0.3, 0.2,
              0.25, 0.05, 0.7,
              0.1, 0.8, 0.1), ncol=3, byrow=T)

# 随机初始点
x <- c(1)

# 转移迭代
for(i in 2:100000){
  xt <- x[i-1]
  y <- sample(1:3, 1, prob=q[xt, ])
  alpha <- p[y] * q[y, xt]
  x[i] <- ifelse(runif(1) < alpha, y, xt)
}

输出结果

1
2
3
4
5
> freq <- table(x)
> freq / sum(freq)
x
      1       2       3 
0.60126 0.30301 0.09573

可以看到样本基本服从目标分布

转移矩阵采样

这里我们直接构造转移矩阵\(Q^*\)进行采样，本质上和MCMC采样相同

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 目标分布pi
p <- c(0.6, 0.3, 0.1)

# 随便取一个Q
q <- matrix(c(0.5, 0.3, 0.2,
              0.25, 0.05, 0.7,
              0.1, 0.8, 0.1), ncol=3, byrow=T)

# 计算转移矩阵
alpha <- t(p * q)
q1 <- alpha * q
q2 <- add_diag(q1)

# 随机初始点
x <- c(1)

# 转移迭代
for(i in 2:100000){
  x[i] <- sample(1:3, 1, prob=q2[x[i-1], ])
}

输出结果

1
2
3
4
5
> freq <- table(x)
> freq / sum(freq)
x
      1       2       3 
0.60221 0.29875 0.09904

错误采样方式

下面展示按照“忽视此轮重新抽样”的方式采样，得到的样本分布无法保证是目标分布

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 目标分布pi
p <- c(0.6, 0.3, 0.1)

# 随便取一个Q
q <- matrix(c(0.5, 0.3, 0.2,
              0.25, 0.05, 0.7,
              0.1, 0.8, 0.1), ncol=3, byrow=T)

# 随机初始点
x <- c(1)

# 转移迭代
i <- 2
while(i <= 10000){
  xt <- x[i-1]
  y <- sample(1:3, 1, prob=q[xt, ])
  alpha <- p[y] * q[y, xt]
  if(runif(1) < alpha){
    x[i] <- y
    i <- i + 1
  } 
}

输出结果

1
2
3
4
5
6
7
8
9
> freq <- table(x)
> freq / sum(freq)
x
     1      2      3 
0.6799 0.2015 0.1186 

# 对比Q'每一行概率不足1的部分
> 1 - apply(q1, 1, sum)
[1] 0.82550 0.89825 0.81900

可以看出，\(Q'\)中第二行有更多概率会被归入对角线中，而“忽视此轮重新抽样”的方式会将这部分概率抹去。因此得到的样本中，状态2的概率下降0.1左右，是第二行不足1的部分比其他两行多0.1左右造成的。

MCMC采样算法改进

上述MCMC算法采样代码中显示，需要100000次迭代才能产生较满意的结果，这是接受率\(\alpha\)太低、导致太多原地踏步造成的。如果能把接受率调高一些，状态之间的转移会更加灵活，需要的迭代次数也可大大降低。

我们先来回顾一下细致平稳条件

\[ \alpha_{ij}=\pi(j) Q_{ji} \]

\[ \pi(i) Q_{ij} \alpha_{ij} =\pi(j) Q_{ji} \alpha_{ji} \]

如果我们将\(\alpha\)整体扩大\(k\)倍，显然细致平稳条件仍然成立，则

\[Q'_ {ij}=kQ_{ij}\alpha_{ij}\]

这个\(Q'\)的每一行加和也不能保证等于1；同时我们在扩大\(\alpha\)时，需要保证\(Q'\)的每一行不超过1，因此扩大的最大程度只能是：使\(Q'\)的某一行加和为1，同时其他行加和不超过1。这样扩大后，可以再将每一行不足1的部分补到对角线上。这个改进效果非常好，我们来看代码

1
2
3
4
5
6
7
8
9
10
11
# 目标分布pi
p <- c(0.6, 0.3, 0.1)
# 随便取一个Q
q <- matrix(c(0.5, 0.3, 0.2,
              0.25, 0.05, 0.7,
              0.1, 0.8, 0.1), ncol=3, byrow=T)
# 计算新的q
alpha <- t(p * q)
q1 <- alpha * q
q3_temp <- 1/max(apply(q1, 1, sum)) * q1
q3 <- add_diag(q3_temp)

先来看看新的转移矩阵\(Q^*\)如何收敛到目标分布

1
2
3
4
5
6
7
8
9
10
11
12
13
# 现在的方式迭代20次效果已经很好
> q3 %^% 20
          [,1]      [,2]       [,3]
[1,] 0.6001387 0.2999037 0.09995757
[2,] 0.5998074 0.3001337 0.10005891
[3,] 0.5997454 0.3001767 0.10007784

# 之前的方式迭代50次效果仍不好
> q2 %^% 50
          [,1]      [,2]      [,3]
[1,] 0.6185267 0.2871386 0.0943347
[2,] 0.5742771 0.3178573 0.1078656
[3,] 0.5660082 0.3235969 0.1103949

新的\(Q^*\)只需要20次就可以达到很好的效果，之前则需要上百次。

1
2
3
4
5
6
7
8
9
10
11
> q2
       [,1]   [,2]  [,3]
[1,] 0.9755 0.0225 0.002
[2,] 0.0450 0.8990 0.056
[3,] 0.0120 0.1680 0.820

> q3
           [,1]      [,2]        [,3]
[1,] 0.86464088 0.1243094 0.011049724
[2,] 0.24861878 0.4419890 0.309392265
[3,] 0.06629834 0.9281768 0.005524862

对比两个\(Q^*\)可以发现，之前的有太大概率集中在对角线上，而改进后的方案则均匀很多。

采样

1
2
3
4
5
6
7
# 随机初始点
x <- c(1)

# 转移迭代
for(i in 2:10000){
  x[i] <- sample(1:3, 1, prob=q3[x[i-1], ])
}

输出结果

1
2
3
4
5
> freq <- table(x)
> freq / sum(freq)
x
     1      2      3 
0.5958 0.3009 0.1033

可以看到，使用新的\(Q^*\)可以用更少的迭代次数达到差不多的精度。

从本节的改进可以看出，虽然给定一个转移矩阵会对应唯一个平稳分布，但是给定一个平稳分布会对应无数转移矩阵，因此要高效生成平稳分布的样本，选择一个好的转移矩阵至关重要。

MH算法

Metropolis-Hastings 算法也是MCMC采样算法的改进，思路和上一节类似，但做法不同。还是回顾细致平稳条件

\[ \alpha_{ij}=\pi(j) Q_{ji} \]

\[ \pi(i) Q_{ij} \alpha_{ij} =\pi(j) Q_{ji} \alpha_{ji} \]

同样，考虑将\(\alpha\)扩大，此处我们不会将\(\alpha\)矩阵所有值扩大相同倍数，而是对称位置扩大相同倍数。观察上述公式，只要\(\alpha_{ij}\)与\(\alpha_{ji}\)扩大相同倍数，细致平稳条件就仍然成立。而\(\alpha\)作为接受率，不能超过1，因此就对每一个对称位置都分别扩大到其中一个为1，另一个不超过1。这就是MH算法。用公式表示如下

\[ \alpha'_ {ij}=\min \left\{\frac{\alpha_{ij}}{\alpha_{ji}}, 1\right\} =\min \left\{\frac{\pi(j) Q_{ji}}{\pi(i) Q_{ij}}, 1\right\} \]

迭代过程与MCMC采样算法相同，只是\(\alpha\)的计算不同而已

1
2
3
4
5
6
7
8
9
10
# 目标分布pi
p <- c(0.6, 0.3, 0.1)

# 随便取一个Q
q <- matrix(c(0.5, 0.3, 0.2,
              0.25, 0.05, 0.7,
              0.1, 0.8, 0.1), ncol=3, byrow=T)

alpha <- t(p * q)
alpha2 <- pmin(alpha / t(alpha), 1)

查看\(\alpha'\)结果

1
2
3
4
5
> alpha2
     [,1]      [,2]       [,3]
[1,]    1 0.4166667 0.08333333
[2,]    1 1.0000000 0.38095238
[3,]    1 1.0000000 1.00000000

采样

1
2
3
4
5
6
7
8
9
10
# 随机初始点
x <- c(1)

# 转移迭代
for(i in 2:10000){
  xt <- x[i-1]
  y <- sample(1:3, 1, prob=q[xt, ])
  alpha_ij <- alpha2[xt, y]
  x[i] <- ifelse(runif(1) < alpha_ij, y, xt)
}

输出结果

1
2
3
4
5
> freq <- table(x)
> freq / sum(freq)
x
     1      2      3 
0.5950 0.3054 0.0996

可以发现，MH算法相比于MCMC采样算法，效率上有很大的提升，与上一节的改进算法差不多。

两种改进算法对比

效果对比

前面两节我们使用了两种方式对MCMC采样算法进行改进，效果差不多，但是只有MH算法留在了教科书中，这是为什么呢？

它们的唯一差别在于\(\alpha\)扩大时的不同

  • 第一种：全局扩大相同比例，限制是\(Q'\)每行加和不能超过1
  • MH：对称位置扩大相同比例，限制是\(\alpha\)值不能超过1

还是把细致平稳条件公式放上来

\[ \alpha_{ij}=\pi(j) Q_{ji} \]

\[ \pi(i) Q_{ij} \alpha_{ij} =\pi(j) Q_{ji} \alpha_{ji} \]

\[ Q'_ {ij} = Q_{ij} \alpha_{ij} \]

按照第一种扩大方式，\(\alpha\)值是可以超过1的；按照第二种扩大方式，\(Q'\)每行加和仍然不会超过1。所以说第一种方式扩大的程度更大，效果可能也会更好，而实际上流传下来的是第二种方法。

这就涉及一个问题：为什么要提出“接受率”这个概念？MCMC算法中不定义接受率也可以转移，思路更清晰、代码更简洁，但它却从“接受率”的角度来写；以MH算法中为了保证接受率有意义，而限制了\(\alpha\)的放大。为什么接受率这么重要？

因为不用接受率的版本无法应用到实际问题之中。

连续情形

为了说明马尔科夫的收敛性，我们引入转移矩阵，一直用这个离散的例子进行说明，而MCMC算法创造时要解决的问题显然不是生成一个简单的离散分布。MCMC算法以及改进的MH算法是用于生成一些非常见分布的随机样本，这些分布可以是离散的也可以是连续的，可以有无穷多取值。我们来看看连续版本的公式

目标：生成分布\(\pi(x)\)的样本，使用工具分布\(q(y|x)\)，计算接受率如下

\[ \text{MCMC:}\quad \alpha(x, y)=\pi(y) q(x|y) \]

\[ \text{MH:}\quad \alpha(x, y)=\min \left\{1, \frac{\pi(y) q(x | y)}{\pi(x) q(y | x)}\right\} \]

细致平稳条件

\[ \pi(x) q(y|x) \alpha(x,y) =\pi(y) q(x|y) \alpha(y, x) \]

这里的工具分布(proposal)就是原来的转移矩阵，从状态\(i\)到状态\(j\)转移一次的过程，就相当于从条件分布\(q(y|x=i)\)中生成一个样本\(j\)。下面对比两种改进方式

MCMC及MH算法过程

MCMC及MH算法的思想就是，直接从目标分布\(\pi(x)\)中生成样本非常困难，于是我们找来一个条件分布\(q(y|x)\)，从这个分布中生成样本比较容易，但这个条件分布是随便找的，不可能用它转移得到的样本都满足要求，所以要通过接受率进行筛选。

这个过程中，每一次迭代都有一个初始值\(i\)，从工具分布\(q(y=j|x=i)\)中抽取样本\(j\)，有了\(i,j\)和\(\pi\)与\(q\)的公式形式后\(\alpha(i,j)\)显然可以算出，整个生成过程可以实现。

第一种改进的方法

第一步：计算

\[ q'(y|x) = q(y|x)\alpha(x,y) \]

第二步：从\(q'\)计算\(q^*\)。要对任意的\(i\)，将\(q'(y|x=i)\)不足1的部分补到\(q'(y=i|x=i)\)上。

这两步都存在问题

  • 第二步中要算出不足1的部分需要对这个函数积分，这个积分过程繁琐不说，还不一定能实现
  • 第一步中计算的\(q'\)是多个式子相乘后的结果，形式可能非常复杂，导致无法从这个分布中抽样，违背了引入\(q\)的初衷

因此在连续问题中，第一种改进方案几乎不可行，这就是接受率重要的原因。细想一下，两种做法的区别在于

  • 第一种是事先把原材料都准备好，在迭代过程中只要带入表达式计算，这在一般问题中是不现实的
  • MH算法的思想是遇到了再现算

MH算法与Rejection Sampling的关系

如果对Rejection Sampling不了解可以先参考这篇文章。

回顾Rejection Sampling

要生成目标分布\(p(x)\)的样本，直接生成非常困难，我们可以从一个简单的分布\(q(x)\)中不断生成样本，再设置一个接受率对每次生成的样本进行筛选。

算法步骤

  • 用一个合适的分布\(q(x)\)，找到一个数\(k\)，使对所有\(x\)值，\(kq(x)\)都比\(p(x)\)大
  • 下面过程迭代，直到获得n个样本
    • 从\(q(x)\)中生成一个样本\(z\)
    • 从\(0-kq(z)\)的均匀分布生成\(u\)
    • 如果\(u < p(z)\)则接受样本\(z\)
    • 如果\(u > p(z)\)则拒绝样本\(z\)，即忽视此轮迭代

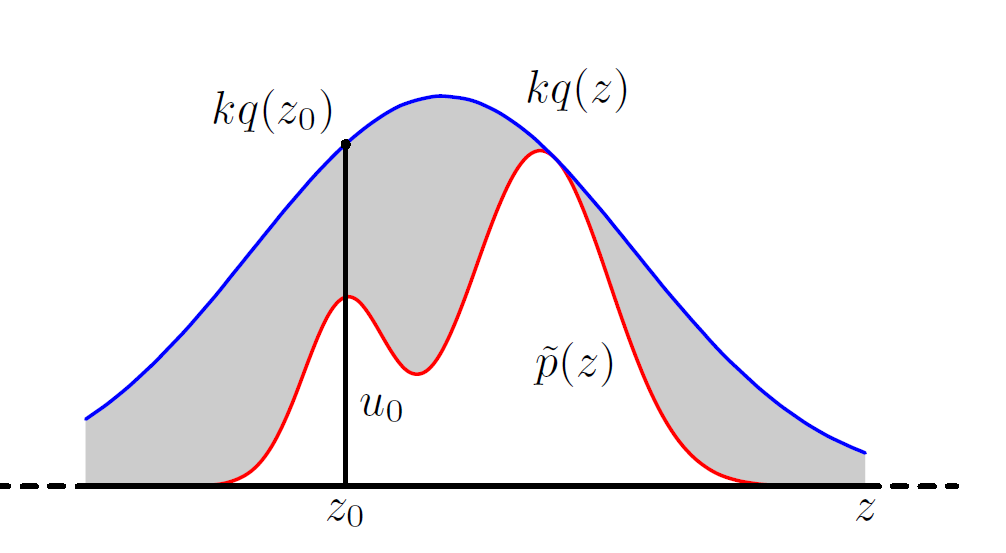
在这张图中即筛选时落入灰色区域则拒绝，落入白色区域则接受。Rejection Sampling非常符合直觉。

补充

  • 什么样的\(q\)是合适的？只要能找到这么一个\(k\)，使\(kq(x)\)总比\(p(x)\)大就行
  • 那么什么时候会找不到呢？比如目标分布是\(t\)分布，而你如果想让\(q\)服从正态分布，则无法找到这个\(k\)；因为\(t\)分布厚尾，在\(|x|\)很大时正态分布下降的速度太快，无论用多大的\(k\)都没办法让它在\(t\)分布上方。
  • 即使是合适的\(q\)也有好坏之分，评定原则是与目标分布越相近的越好，因为拒绝区域越少，算法效率越高

MH算法与Rejection Sampling的类似点

  1. 二者的抽样过程类似
  • 都是用一个工具分布产生样本，设置一个接受率
  • 但不同的是前者拒绝后会使用上一轮的值，而后者会忽视此轮，因此二者无法等价
  • 也不能说哪个的效率更高，因为废弃样本和停滞在原地都不利于抽样
  1. 二者要解决的问题类似

它们都用于对不常见分布进行抽样

  • 可以是那些已知\(p(x)\)函数形式，但难以建立与均匀分布之间联系的分布
  • 也可以是\(p(z)=\frac{1}{Z_{p}} \widetilde{p}(z)\)这种形式，即我们知道\(\widetilde{p}(z)\)的形式，但是不知道\(Z_p\)的值（\(Z_p\)是一个常数，用于将概率加总归一化到1），所以无法知道确切的分布。贝叶斯统计中的后验分布一般都是这种形式，如果\(\widetilde{p}(z)\)的积分难求，则\(Z_p\)无法计算。从两个方法的过程来看，我们不需要知道\(Z_p\)的值即可对这个分布进行采样

举例：已知先验分布\(\theta \sim Gamma(\alpha, \beta)\)，\(Y_1,...,Y_n\)样本来自\(N(\theta,1)\)，要生成服从后验分布的样本。

特殊工具分布

如果MH算法的工具分布\(q(y|x)\)特殊，则接受率可以简化

\[ \alpha(x, y)=\min \left\{1, \frac{\pi(y) q(x | y)}{\pi(x) q(y | x)}\right\} \]

  1. 独立

即工具分布是独立于\(x\)的，\(q(y|x)=q(y)\)，接受率公式如下

\[ \alpha(x, y)=\min \left\{1, \frac{\pi(y) q(x)}{\pi(x) q(y)}\right\} \]

此时，所有候选样本都是从同一个分布生成，更加类似Rejection Sampling，因为它的接受率可以写成这种形式

\[ \alpha(y) = \frac{\pi(y)}{k q(y)}, \quad\text{其中} k = \max_y \frac{\pi(y)}{q(y)} \]

但是二者依然不同。

  1. 对称（这部分与对比无关，只是补充这种特殊情况）

即\(q(y|x)=q(x|y)\)，则

\[ \alpha(x, y)=\min \left\{1, \frac{\pi(y) }{\pi(x) }\right\} \]

一个对称分布的例子：\(y|x\sim N(x, 1)\)，则对已知的\(x,y\)有\(q(y|x)=q(x|y)\)

全局与局部

  • Rejection Sampling是从全局找目标分布的近似，用其密度函数的包络线生成样本再筛选，但是全局近似可能在很多位置与目标相差太远，而且工具分布选择要考虑所有取值来确定
  • 而MH算法每次使用的工具分布不同，相当于是在局部找近似，在每一步确定工具分布时不需要考虑目标整体，顾虑较少；同时也不需要考虑\(k\)能否计算

高维情况

二者都可以直接应用到多元分布采样上，只是一般此时接受率都非常低，算法效率不高。MH算法的一个优势在于Gibbs采样的扩展，可以对一些多元分布高效采样。

回到最初的话题，已知目标分布，我们希望找到一个转移矩阵（条件概率）满足细致平稳条件。在之前的问题中，这个转移矩阵需要各种构造，但是在多元分布采样中，它是现成的，完美满足细致平稳条件，是以算法中甚至没有“接受率”的存在。

Gibbs采样的细致平稳条件公式如下

\[ \begin{array}{l} {p(x_{1}, y_{1}) p(y_{2} | x_{1})= p(x_{1}) p(y_{1} | x_{1}) p(y_{2} | x_{1})} \\ {p(x_{1}, y_{2}) p(y_{1} | x_{1})= p(x_{1}) p(y_{2} | x_{1}) p(y_{1} | x_{1})} \end{array} \]

所以

\[ p(x_{1}, y_{1}) p(y_{2} | x_{1})=p(x_{1}, y_{2}) p(y_{1} | x_{1}) \]

工具分布用的是\(p(y_2|x_1)\)，而不是\(p(x_2,y_2|x_1, y_1)\)，是因为要沿着与轴平行方向转移，固定其他轴的值不变。只要每次沿着与轴平行方向转移，都满足细致平稳条件，得到的样本是服从目标分布。

gibbs采样适用于多元分布较难抽样，但容易从条件分布中抽样的情况。举例如下

要生成这个分布的样本

\[ p(x, y)=\frac{n !}{(n-x) ! x !} y^{(x+\alpha-1)}(1-y)^{(n-x+\beta-1)}, \quad x \in\{0, \ldots, n\}, y \in[0,1] \]

这不是常见分布，难以直接抽样，但是它的条件分布都是常见分布

  • \(p(x | y) \equiv \operatorname{Bin}(n, y)\)
  • \(p(y | x) \equiv \operatorname{Beta}(x+\alpha, n-x+\beta)\)

参考资料

参考资料

继续阅读