假设检验回顾
本节我们回顾一下本科数理统计中学习的假设检验。
举一个例子,我们现在想要知道厦门市市民的平均身高是不是\(\mu_0 = 165cm\),我们可以采集一组数据\(X_1, X_2, ..., X_n\)(足够多),计算这组数据的均值\(\bar X_n\),看这个均值离\(\mu_0\)近不近。这是假设检验的基本思想。
用数学符号表示就是,要检验
\[H_0: \mu = \mu_0 \quad v.s. \quad H_1: \mu \neq \mu_0\] 在大样本的情况下,由中心极限定理可以保证样本均值服从正态分布
\[\bar X_n \stackrel{d}{\rightarrow} N(\mu, Var)\] 此时我们会假设\(H_0\)成立,则有
\[\frac{\bar X_n-\mu_0}{\sqrt{Var}} \stackrel{d}{\rightarrow} N(0, 1)\] 这里\(Var\)如果已知就直接使用,如果未知就用样本方差估计,这不是我们关注的重点。总之,将当前样本均值带入,我们可以计算出\(\frac{\bar X_n-\mu_0}{\sqrt{Var}}\)值。直观上来想,如果这个值非常大或者非常小,则说明出现这个\(\bar X_n\)的概率非常小(处于正态分布的尾端),我们就不敢相信最初假设的\(H_0\)是正确的。为了定义什么时候是“非常大非常小”,我们设置犯第一类错误概率不能超过\(\alpha=0.05\),对应标准正态分布\(\pm 1.96\)作为阈值,超出这个阈值则拒绝原假设。
如果换一个检验问题
\[H_0: \mu = \mu_0 \quad v.s. \quad H_1: \mu > \mu_0\] 则只有样本均值过大时才拒绝原假设,\(\alpha=0.05\)的范围也只从右边取。
再考虑对方差进行检验时,得到的统计量服从的是卡方分布,检验方法如出一辙,从两侧找拒绝域。
看起来这套理论已经理解通透了,但是不妨考虑这样一个问题:为什么拒绝域要从两侧取,从分布中间任何一个地方都可以取到一块区域概率是0.05,从两侧取的理论依据是什么,换一个分布形式还是从两侧取吗(比如原假设变成均匀分布)?不是的话怎么取?
UMP Test
首先定义两类错误
- 第一类错误:\(H_0\)真的正确的情况下,我们的判断方法拒绝\(H_0\)的概率(\(H_0\)成立时落入拒绝域的概率)
- 第二类错误:\(H_1\)正确的情况下,我们的判断方法却接受了\(H_0\)的概率
一个好的检验方法需要使两类错误都尽可能小,但是犯两类错误的概率往往是此消彼长的关系,因此我们采用这样的方法:控制第一类错误概率不超过0.05的情况下,使犯第二类错误的概率尽可能小。这种检验方法称为UMP Test(uniform most powerful test).
我们平时使用的检验都是基于UMP Test,但是由于符合直觉,使用时常常会忽略其本质。
下面我将从简单情况开始推广,理顺假设检验的逻辑。
简单假设
首先,要纠正一个误区。我们进行假设检验,看起来在判断一个值是否等于某给定值,但是其本质是在看一个统计量服从哪个分布(服从\(H_0\)对应分布还是\(H_1\))。
前面我们提到的对\(\mu\)进行的检验,其实是在对\(\bar X_n\)的分布进行检验,\(\mu\)是其正态分布中的一个参数,由于参数可以唯一确定分布,所以这里检验分布就可以当做检验参数了。
下面,我们来看一个例子,只有一个样本\(X\),它服从正态分布\(N(\mu, 1)\),使用参数\(\mu\)检验如下
\[H_0: \mu = 0 \quad v.s. \quad H_1: \mu = 1\] 这是假设检验中最简单的一个例子,前面提到的多个样本、\(H_1:\mu \neq 0\)、\(H_1:\mu > 0\)都是它的推广。
这里我们引入简单假设的概念:\(H_0/H_1\)中包含的分布只有一个的假设
- \(H_1:\mu \neq 0\)显然不是一个简单假设,因为这个假设的\(\mu\)的值可以取很多种,也就对应着很多个分布
- \(H_0: \mu = 0\)就是一个简单假设
我们再来看另一个例子,这是两个概率密度函数曲线
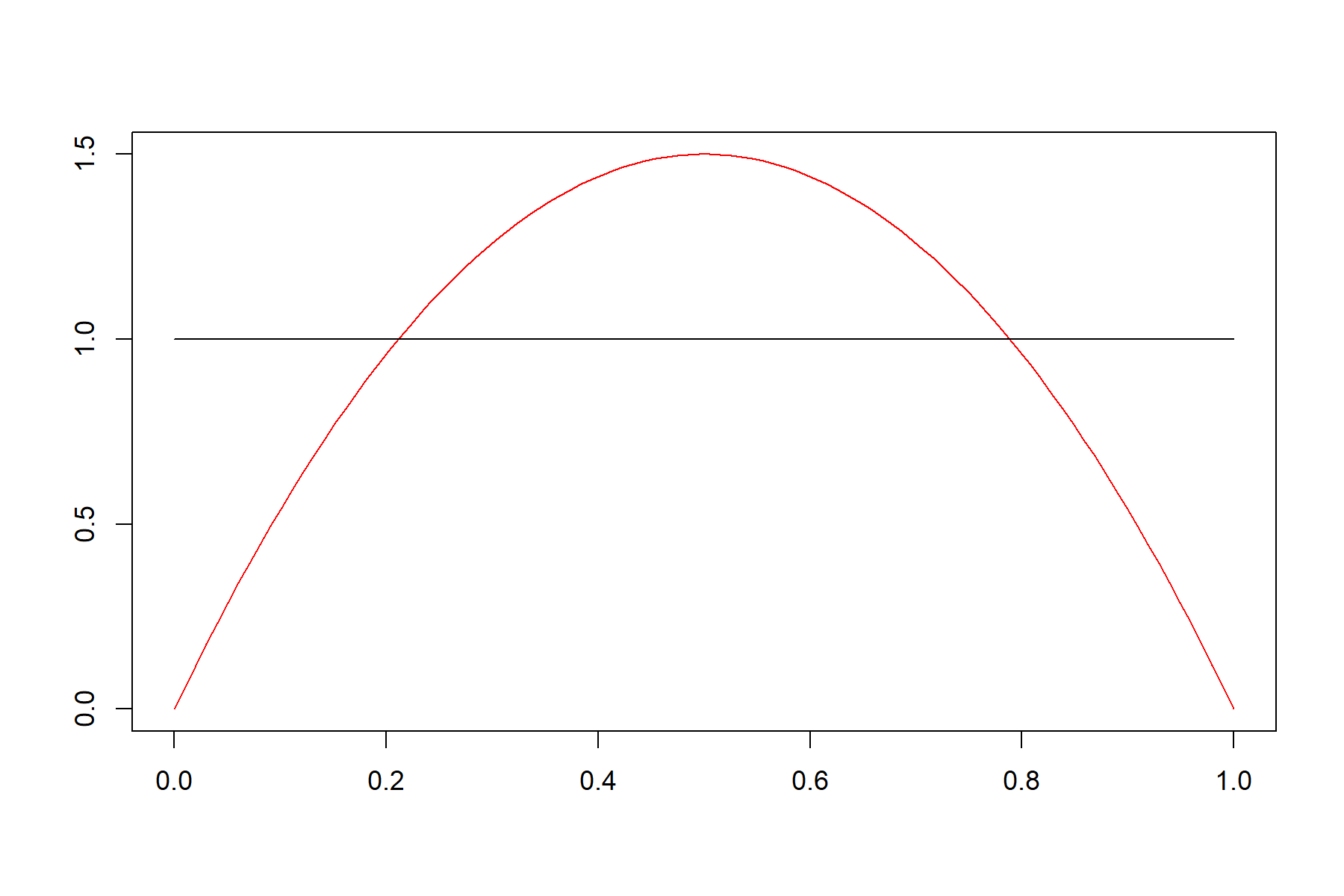
图中黑线表示\(H_0\)的分布,红线表示\(H_1\)的分布。现在我们要找到它的检验规则,及判断一个样本服从黑线分布还是服从红线分布。
面对这样的问题会发现,之前学过的那种应对正态分布的套路已经没有用了,我们不能再随意地取两端的区域作为拒绝域,只能从假设检验的本质出发,寻找有效的检验方法。
我们需要在控制第一类错误概率不超过0.05的情况下,使犯第二类错误的概率尽可能小。也就是说,我们要找到一个区间,这个区间对应的\(H_0\)分布概率不超过0.05,而\(H_1\)分布概率尽可能大。反映在图中即为找一块区域,区域内黑线所围面积不超过0.05,而红线内面积尽可能大。所以最中间那块使黑线面积为0.05的区间就是我们要找的拒绝域,这个结果显然和正态分布情况下取两端作为拒绝域不同。这里是通过直观理解找到的这块区域,下面我们会为这个方法提供理论支撑和计算方式。
NP Lemma
NP Lemma可以说是假设检验的基石,这里不打算写出引理的数学表达式,只是简述其思想。
NP Lemma证明了在\(H_0\)和\(H_1\)都是简单假设的情况下,UMP Test一定存在,而且形式是这样的:
要找到c,当\(\frac{f_1(X)}{f_0(X)}>c\)就拒绝原假设,其中\(f_1(X)\)和\(f_0(X)\)分别表示\(H_1\)和\(H_0\)的概率密度函数。
(就像正态分布时\(X_n>c\)拒绝原假设一样)
也就是说,找到\(\frac{f_1(X)}{f_0(X)}\)比值最大的那5%范围,这个范围内拒绝原假设,这样的检验方法是最好的检验(UMP Test)。
这个引理其实也非常符合直觉,\(f_1\)在分母上越大越好(犯第二类错误的概率更小),\(f_0\)在分子上,越小越好(犯第一类错误的概率更小)。
现在回过头来看上一节最后的那个例子,会发现用现在这种计算方式就会得到中间的那片区域。即\(\frac{6(x-x^2)}{1}>c\)再加上黑线围成面积是0.05的条件,就可以解出\(c\)和\(x\)的范围。
不仅如此,本科学过的对正态分布和卡方分布的检验也都是基于这个方法,只是经过了一些定理的扩展。扩展我们最后再说,现在先换一个思路,理解一下这个引理。
似然比检验
现在忘掉前面所说的假设检验的内容,回想一下参数估计中的MLE(极大似然估计法)方法。
参数估计是,有一个带有未知参数\(\theta\)的分布,现在得到一组基于该分布的iid数据\(X_1, X_2, ..., X_n\),要估计分布的参数。MLE的思想是:计算出现当前这些样本出现的概率,这个概率结果是带有参数\(\theta\)的一个表达式,通过求解表达式极大值来确定参数\(\theta\)。
现在,我们想知道\(\theta\)等于0还是等于1,按照刚才的思路,只需要分别计算\(\theta = 0\)和\(\theta = 1\)时当前样本出现的概率,做个比较就可以知道\(\theta\)取哪个值比较好。(做检验时,想要拒绝\(H_0\)需要非常谨慎,要\(f_1\)比\(f_0\)大足够多才可以拒绝,因此有了\(>c\)之说)
我们来看一下拒绝域的表达式
\[\frac{f_1(X, \theta)}{f_0(X, \theta)}=\frac{\prod_{i=1}^{n} f_1(X_i,\theta)}{\prod_{i=1}^{n} f_0(X_i, \theta)} > c\]
这种用似然函数作比进行的检验称为似然比检验。这里形式和NP Lemma时一样的,这种情况下,似然比检验是UMP Test。
扩展延伸
1.扩展到多样本
第一种理解:从NP Lemma的角度来看,单个样本直接用这个分布概率来算,多个分布则用联合分布概率来算,因为样本一般都是iid的,所以只是多个概率相乘计算而已。
那么为什么正态分布检验\(\mu\)会用\(\bar X_n\)来算呢?是因为\(\frac{f_1(X, \theta)}{f_0(X, \theta)}>c\)把正态分布形式带入可以化简成只用\(\bar X_n\)表示。
更进一步理解,考虑充分统计量的定义,二者作比得到的一定是关于充分统计量的表达式,所以NP Lemma找到的UMP Test结果总是可以写成对充分统计量的判断,如果分布有一些单调性质,则UMP Test会非常简洁(就像正态分布一样只是\(\bar X_n\)大于一个数这样)。
第二种理解:直接考虑\(\bar X_n\)的分布,这个分布也是带有\(\mu\)参数的,而这里只获得了一个\(\bar X_n\)的样本,于是就转化为单样本的情况了。
2.\(H_1\)的扩展
NP Lemma只是帮助我们找到了\(H_0\)和\(H_1\)都是简单假设时的UMP Test,但是像我们通常见到的
\[H_0: \mu = \mu_0 \quad v.s. \quad H_1: \mu > \mu_0\]
\[H_0: \mu = \mu_0 \quad v.s. \quad H_1: \mu \neq \mu_0\]
则需要更多定理来保证,虽然最后可以证明检验方法和
\[H_0: \mu = \mu_1 \quad v.s. \quad H_1: \mu = \mu_2\]
没有什么区别(对正态分布来说都是找\(|\bar X_n|>c\)这样的区域)。
由于推广过程过于复杂,这里不展示证明过程。这些复杂的检验只适用于某些特定分布族,他们会有一些单调特性,才可以保证\(H_1\)无论取什么样的分布,检验方法都和简单假设时相同。