傅里叶级数与傅里叶变换（一）

本文由于篇幅原因拆成两篇，下一篇见这里。

傅里叶级数

在一定条件下，任意周期为\(T=\frac{2\pi}{w}\)的函数\(f(t)\)都可以用一系列正弦函数展开，此时需要满足\(T\)也要是这些正弦函数的周期（不要求正弦函数周期是\(T\)，只要能被\(T\)整除就行了），如下所示

\[ f(t) = A_0 +\sum_{n=1}^\infty A_n\sin(nwt+\varphi_n) \tag{1} \]

（当\(f(x)\)满足这个条件时，它的傅里叶级数收敛到\(f(x)\)，也就是说在这个条件满足的情况下，\(f(x)\)可以写成傅里叶级数形式。）

收敛定理-狄利克雷充分条件

设周期函数\(f(x)\)的周期为\(T\)，如果\(f(x)\)满足在一个周期内连续或只有有限个第一类间断点，并且至多只有有限个极值点，则\(f(x)\)的傅里叶级数收敛，且有

• 当\(x\)是\(f(x)\)的连续点时，级数收敛于\(f(x)\)
• 当\(x\)是\(f(x)\)的间断点时，收敛于

\[ \frac{f(x-0)+f(x+0)}{2} \]

这表示，只要\(f(x)\)在区间\([-\frac T2, \frac T2]\)上至多只有有限个第一类间断点，并且不作无限次振动即可。我们通常见到的函数都满足这个条件，所以可以直接用公式计算系数，将函数写成傅里叶级数形式。

注：第一类间断点表示间断点处左右极限都存在，包括可去间断点和跳跃间断点。

这表示即使是方波也可以通过弯曲的正弦函数逼近，如下图所示（图片来自wiki）

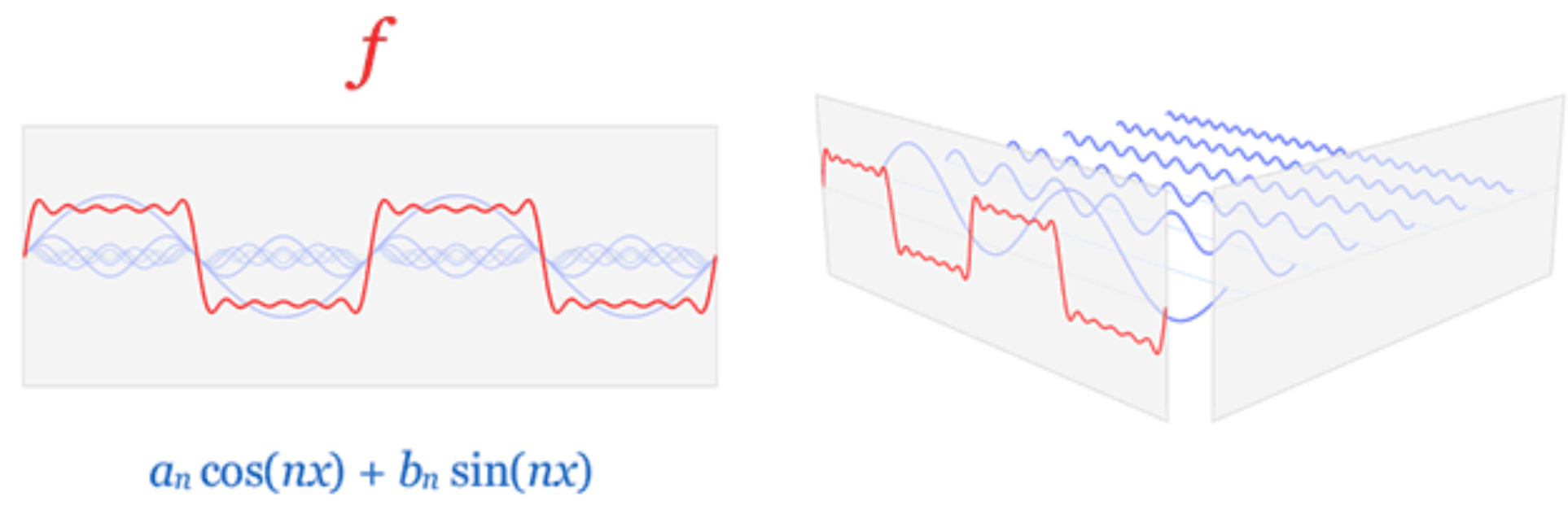
上式说明，如果我们知道等式右侧的所有三角函数信息，就可以知道\(f(t)\)的的全部信息。如果我们想将\(f(t)\)分解成这种加和的形式，就是想求每个三角函数的三个部分信息：振幅\(A_n\)，频率\(\frac{n}{T}\)，初相\(\varphi_n\)。\(f(t)\)周期已知则每个三角函数的频率已知，而振幅\(A_n\)和初相\(\varphi_n\)不好算，我们可以对右式加以变形转化问题。由和角公式可知 \[ A_n\sin(nwt+\varphi_n)=a_n\cos(nwt)+b_n\sin(nwt) \tag{2} \] 其中\(a_n=A_n\sin\varphi_n\)，\(b_n=A_n \cos\varphi_n\)。这样初相\(\varphi_n\)的信息就被移到了系数之中。

再记\(A_0=\frac{a_0}{2}\)，则\(f(t)\)的展开公式可以写成 \[ \begin{align} f(t)&=\frac{a_0}{2}+ \sum_{n=1}^\infty \left[a_n \cos(nwt)+b_n \sin(nwt)\right]\\ &=\frac{a_0}{2}+ \sum_{n=1}^\infty \left[a_n \cos \frac{2\pi nt}{T}+b_n \sin\frac{2\pi nt}{T}\right] \tag{3} \end{align} \] 问题就转化为求\(a_n\)和\(b_n\)，利用三角函数系正交的性质，可以通过积分计算出\(a_n\)和\(b_n\)。

\[ \begin{align} a_n = \frac{2}{T} \int_{-\frac T2}^{\frac T2} f(t) \cos \frac{2n\pi t}{T}\mathrm{d}t, \quad n=0, 1, 2, \cdots\\ b_n = \frac{2}{T} \int_{-\frac T2}^{\frac T2} f(t) \sin \frac{2n\pi t}{T}\mathrm{d}t, \quad n=1, 2,3, \cdots\\ \end{align} \]

点击查看：

三角函数系

\[ 1, \cos x, \sin x, \cos 2x, \sin 2x, \cdots, \cos nx, \sin nx, \cdots \] 在区间\([-\pi, \pi]\)上正交，即两两乘积在这个区间内积分为0。具体如下 \[ \begin{align} &\int_{-\pi}^\pi \cos nx \mathrm{d}x = 0, \quad n=1,2,3,\cdots\\ &\int_{-\pi}^\pi \sin nx \mathrm{d}x = 0, \quad n=1,2,3,\cdots\\ &\int_{-\pi}^\pi \cos mx \cos nx \mathrm{d}x = 0, \quad m\neq n, m, n=1,2,3,\cdots\\ &\int_{-\pi}^\pi \sin mx \sin nx \mathrm{d}x = 0, \quad m\neq n, m, n=1,2,3,\cdots\\ &\int_{-\pi}^\pi \sin mx \cos nx \mathrm{d}x = 0, \quad m, n=1,2,3,\cdots\\ \end{align} \] 证明示例：通过积化和差公式，有 \[ \int_{-\pi}^\pi \cos mx \cos nx \mathrm{d}x = \frac12 \int_{-\pi}^\pi [\cos (m+n)x +\cos (m-n)x] \mathrm{d}x = 0 \] 除了上述公式外，还有下面两个公式 \[ \begin{align} &\int_{-\pi}^\pi \cos^2 nx \mathrm{d}x = \pi, \quad n=0,1,2,3,\cdots\\ &\int_{-\pi}^\pi \sin^2 nx \mathrm{d}x = \pi, \quad n=1,2,3,\cdots\\ \end{align} \]

傅里叶级数系数求解

对于周期为\(T\)的函数\(f(t)\)，首先进行一步变换，将周期变成\(2\pi\)。令\(z=\frac{2\pi t}{T}\)，则\(f(t)\)可写成 \[ F(z)=\frac{a_0}{2}+ \sum_{n=1}^\infty (a_n \cos nz+b_n \sin nz ) \] （其实就是将\(f(t)\)公式中\(\frac{2\pi t}{T}\)统一写成\(z\)，这时式子是关于\(z\)的函数，所以写成\(F(z)\)，实际上\(F(\frac{2\pi t}{T})=f(t)\)。）

第一步，两侧同时在\([-\pi, \pi]\)区间上积分，由三角函数系正交性质可消去0项，得到\(a_0\) \[ a_0=\frac1\pi \int_{-\pi}^\pi F(z)\mathrm{d}z \] 第二步，两侧同时乘\(\cos nz\)，再积分可得 \[ a_n=\frac1\pi \int_{-\pi}^\pi F(z)\cos nz \mathrm{d}z \] 第三步，两侧同时乘\(\sin nz\)，再积分可得 \[ b_n=\frac1\pi \int_{-\pi}^\pi F(z)\sin nz \mathrm{d}z \]

其中第一步可以统一到第二步里，再将\(z\)换成\(\frac{2\pi t}{T}\)可得

\[ \begin{align} a_n = \frac{2}{T} \int_{-\frac T2}^{\frac T2} f(t) \cos \frac{2n\pi t}{T}\mathrm{d}t, \quad n=0, 1, 2, \cdots\\ b_n = \frac{2}{T} \int_{-\frac T2}^{\frac T2} f(t) \sin \frac{2n\pi t}{T}\mathrm{d}t, \quad n=1, 2, 3,\cdots\\ \end{align} \]

有了\(a_n\)和\(b_n\)，就可以计算振幅\(A_n\)和初相\(\varphi_n\)，我们就完成了\(f(t)\)的分解。

补充说明

• 直观理解\(a_n\)和\(b_n\)的计算过程：将三角函数系看做基，要求的是\(f(t)\)的坐标，即\(f(t)\)在各个基上的投影，用\(f(t)\)和基做内积来计算，积分相当于内积运算。
• 当\(f(t)\)为奇函数时，傅里叶系数\(a_n=0, n=0,1,\cdots\)，此时傅里叶级数展开全由\(\sin\)构成，且没有常数项
• 当\(f(t)\)为偶函数时，傅里叶系数\(b_n=0, n=1,2,\cdots\)，此时傅里叶级数展开全由\(\cos\)构成
• 有时会看到计算\(a_n,b_n\)时积分范围是\([0,T]\)，这也是一样的，都是在一个周期内积分，三角函数系正交性在\([0,T]\)下也是成立的
• 有时会看到一种写法：\(a_n, b_n\)表达式前没有\(\frac{2}{T}\)项。这时会发现\((3)\)式中有一个\(\frac2T\)被提到最前面了，所以\(a_n, b_n\)就是未被scaled的项
• 连续函数\(f(t)\)展开后是离散的加和；如果将\(a(\frac{n}{T})\)看做一个函数（系数-频率函数），自变量只取离散的值；可以发现当\(T\)逐渐增大时，这个函数的定义域会越来越密集，极限下覆盖整个坐标轴。也就是说，当\(T\rightarrow \infty\)时，\(f(t)\)是非周期函数，系数-频率函数是连续的
  • 频率的解释：展开每一项的周期是\(2\pi / \frac{2n\pi}{T}=\frac{T}{n}\)，频率是周期的倒数，即\(\nu=\frac{n}{T}\)，所以上面的系数-频率函数应写成\(a(\nu)\)
  • 频率的含义：比如周期是\(T\)，说明经过\(T\)这么长时间能转一圈；频率就是\(1\)这么长时间能转多少圈
  • 有的资料里自变量用的是角频率。角频率是频率乘\(2\pi\)，上面公式中的\(w\)就是角频率；考虑角度，\(T\)这么长时间能转\(2\pi\)角度，角频率就表示\(1\)这么长时间能转多大角度。
• 对于非周期函数
  • 如果定义在有限区间，则可以通过周期延拓（复制这段到无穷区间）变成周期函数，得到傅里叶级数后再对定义域进行限制。此时展开式仍是在用级数表示。
    • 此处要注意，定义在有限区间，表示区间以外无定义；如果是区间以外都为0则是定义在无限区间上的非周期函数
  • 如果定义在无限区间，则展开用积分表示（傅里叶积分）
• 本文偏重直观理解，若有证明也只是为了加深理解；对于一些极限收敛、间断点等理论方面内容读者可自行参考教材

傅里叶级数的复数形式

如果有两个周期函数\(f(t)\)和\(g(t)\)，要在傅里叶级数下计算二者的乘积，上面的展开方式就比较难算，要用各种积化和差公式推导，此时我们可以将傅里叶级数写成复数形式，利用欧拉公式 \[ e^{ix}=\cos x+i \sin x \] 我们的目的是将式\((3)\)中的正弦余弦项都换成\(e^{ix}\)形式。由欧拉公式可知 \[ \begin{align} \cos x &= \frac{e^{ix} + e^{-ix}}{2}\\ \sin x &= \frac{e^{ix} - e^{-ix}}{2i}=-\frac{i}{2}(e^{ix} - e^{-ix}) \end{align} \] 因此式\((3)\)可写成 \[ \begin{align} f(t)&=\frac{a_0}{2}+ \sum_{n=1}^\infty \left[a_n \cos \frac{2\pi nt}{T}+b_n \sin\frac{2\pi nt}{T}\right] \\ &=\frac{a_0}{2}+\sum_{n=1}^\infty \left[ \frac{a_n}{2} (e^{i\frac{2\pi nt}{T}}+e^{-i\frac{2\pi nt}{T}}) -\frac{ib_n}{2} (e^{i\frac{2\pi nt}{T}}-e^{-i\frac{2\pi nt}{T}}) \right]\\ &=\frac{a_0}{2}+\sum_{n=1}^\infty \left[ (\frac{a_n}{2}-\frac{b_n}{2}i) e^{i\frac{2\pi nt}{T}} +(\frac{a_n}{2}+\frac{b_n}{2}i) e^{-i\frac{2\pi nt}{T}} \right]\\ &=c_0 +\sum_{n=1}^\infty \left[ c_n e^{i\frac{2\pi nt}{T}} +c_{-n} e^{-i\frac{2\pi nt}{T}} \right]\tag{4}\\ \end{align} \] 其中 \[ \begin{align} &c_0=\frac{a_0}{2}=\frac{1}{T} \int_{-\frac T2}^{\frac T2} f(t) \mathrm{d}t\\ &\begin{split} c_n=\frac{a_n-i b_n}{2}&= \frac{1}{T} \int_{-\frac T2}^{\frac T2} f(t) \left( \cos \frac{2n\pi t}{T} -i\sin \frac{2n\pi t}{T}\right) \mathrm{d}t\\ &=\frac{1}{T} \int_{-\frac T2}^{\frac T2} f(t) e^{-i\frac{2n\pi t}{T}} \mathrm{d}t , \quad n=1, 2, 3, \cdots \end{split}\\ &\begin{split} c_{-n}=\frac{a_n+i b_n}{2}&= \frac{1}{T} \int_{-\frac T2}^{\frac T2} f(t) \left( \cos \frac{2n\pi t}{T} +i\sin \frac{2n\pi t}{T}\right) \mathrm{d}t\\ &=\frac{1}{T} \int_{-\frac T2}^{\frac T2} f(t) e^{i\frac{2n\pi t}{T}} \mathrm{d}t , \quad n=1, 2, 3, \cdots \end{split}\\\tag{5} \end{align} \] 进一步统一、简化 \[ f(t)=\sum_{n=-\infty}^\infty c_n e^{i\frac{2n\pi t}{T}} \tag{6} \] 其中 \[ c_n=\frac{1}{T} \int_{-\frac T2}^{\frac T2} f(t) e^{-i\frac{2n\pi t}{T}} \mathrm{d}t , \quad n=0, \pm 1, \pm 2, \cdots \tag{7} \] 现在，满足一定条件的周期函数\(f(t)\)都可以表示成\((6)\)式形式。回到本节最开始的问题，如果两个函数相乘，用级数来计算，则\((6)\)式这种形式用指数来成显然方便得多。

如果直接看\((6)\)式可能会有疑惑，\(e\)项展开后是复数形式，\(c_n\)也是复数，而\(f(t)\)是实数，这说明相乘相加后虚部全都消掉了。确实如此，推导的话其实就是\((4)\)式的逆过程；关键点在于，\(n\)取正负对称位置放在一起，可以将虚部消掉。

同时\((6)\)式表明，在周期\(T\)已知的情况下，\(e^{i\frac{2n\pi t}{T}}\)的形式固定，则\(f(t)\)中全部的信息可以由序列\(\{c_n\}\)表示。\(f(t)\)和\(\{c_n\}\)的信息等同

• 已知\(\{c_n\}\)时可以通过\((6)\)式计算\(f(t)\)
• 已知\(f(t)\)时可以通过\((7)\)式计算\(\{c_n\}\)

上面是从代数推导的角度看待等同性，下面我们通过波的叠加来看待\(\{c_n\}\)对\(f(t)\)的表示。此处为了方便理解，暂且将一对\((e^{i\frac{2n\pi t}{T}},e^{-i\frac{2n\pi t}{T}})\)看做一个周期为\(\frac{T}{n}\)的波，要确定这个波的具体形态，还需要振幅\(A_n\)和初相\(\varphi_n\)两个要素，这两个要素可以由\(\{c_n,c_{-n}\}\)计算得到。先说结论（注意到\(c_n\)是复数，且\(c_n\)与\(c_{-n}\)共轭，即模长相等，关于实轴对称）

• 振幅\(A_n\)等于\(c_n\)的模长的两倍
• \(c_{-n}\)对应复平面上一个点，这个点偏离实轴的角度就是初相\(\frac \pi 2-\varphi_n\)

证明之前将\((2)\)式列在这里 \[ \begin{align} A_n&\sin(nwt+\varphi_n)=a_n\cos(nwt)+b_n\sin(nwt) \tag{2}\\ &a_n=A_n\sin\varphi_n \qquad b_n=A_n \cos\varphi_n \tag{8} \end{align} \] 振幅的证明

• 由\((5)\)式可知，\(c_n\)的模长为\(\frac{\sqrt{a_n^2+b_n^2}}{2}\)
• 由\((8)\)式可知，\(A_n^2=a_n^2+b_n^2\)

初相的证明

• \(c_{-n}=\frac{a_n+i b_n}{2}\)，偏离实轴角度\(\theta\)有\(\tan \theta=\frac{b_n}{a_n}\)
• 由\((8)\)式可知\(\tan \varphi_n=\frac{a_n}{b_n}\)

这里证明可能不够严谨，下一节可以看到更合适的解释。这里只是想大概建立起\(c_n\)与振幅初相之间的关系，这样就可以通过复数形式的傅里叶级数确定一系列正弦波，这些正弦波的叠加就是原函数。

傅里叶级数与圆周运动

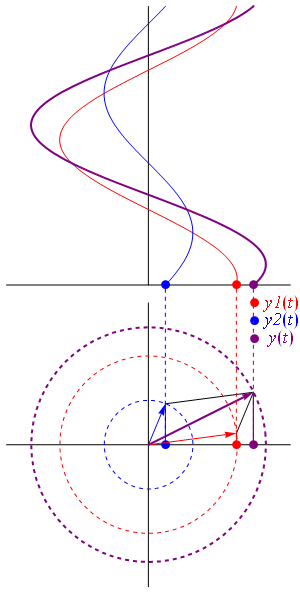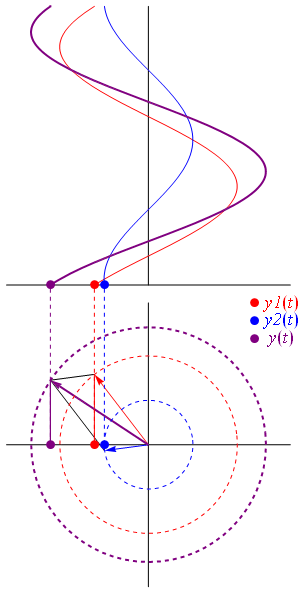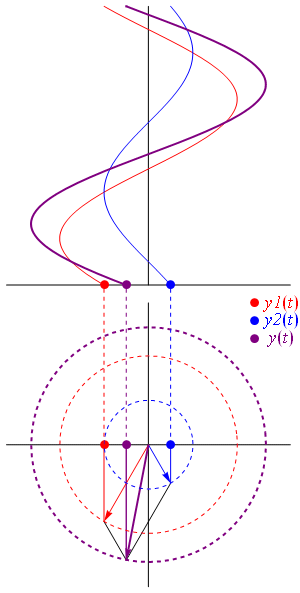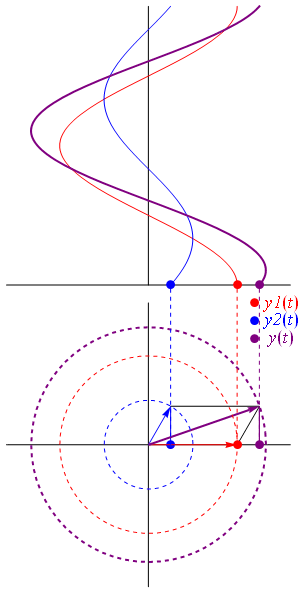
正弦波\(f(t)=\sin t\)可以看做，圆周运动随着时间的流逝，记录下纵轴的值；多个正弦波的叠加则可以看做大圆套小圆转动，如下图所示，图片来自wiki，此外还有一个类似的动图

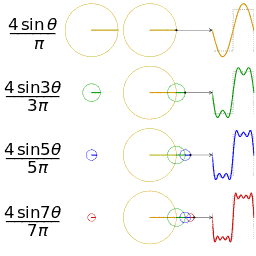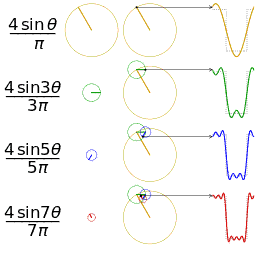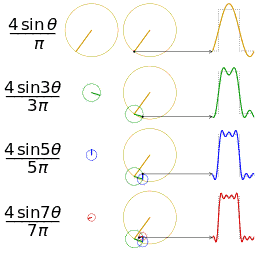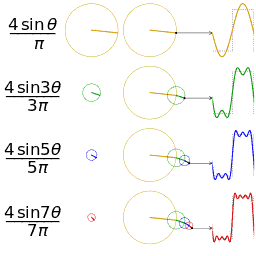
同样的信息，在时域上表现为右侧的周期函数，在频域上表现为左侧固定的圆周运动。

• 在圆周运动中，初相对应初始点，频率对应转动的速度，振幅对应圆的大小。我们只要确定了这三个要素，就可以勾勒出时域中的图像，这是频域向时域的转化。
• 时域向频域转化，就好像对一个复杂的\(f(t)\)，你很难预计下一个时间它会如何变动，但如果告诉你它是由一些确定的圆套在一起运动而形成的，就感觉触及到了本质，事情变得可控。在时域中难以做到的事情，可能在频域中非常简单，这也是傅里叶级数展开的意义所在。

我们经常看到画频谱图的，其实就是振幅-频率图；相位图就是初相-频率图。

上面介绍了\(A_n\sin(nwt+\varphi_n)\)这种形式的波如何通过圆周运动勾勒出\(f(t)\)，下面我们要基于复数形式的傅里叶级数来勾勒\(f(t)\)。首先从欧拉公式说起 \[ e^{it}=\cos t+i \sin t \] 将\(e^{it}\)的值看做在复平面上描点，横轴是实数轴，坐标为\(\cos t\)；纵轴是虚数轴，坐标为\(\sin t\)。则随着时间\(t\)的增大，描点轨迹就是在做逆时针圆周运动，而\(e^{-it}\)则是在做顺时针圆周运动。把\((4)\)式搬过来 \[ f(t)=c_0 +\sum_{n=1}^\infty \left[ c_n e^{i\frac{2\pi nt}{T}} +c_{-n} e^{-i\frac{2\pi nt}{T}} \right] \] 对每个\(n\)来说，两部分在复平面上做圆周运动，\(c_n\)是个复数可以画在复平面内，则\(c_n e^{i\frac{2\pi nt}{T}}+c_{-n} e^{-i\frac{2\pi nt}{T}}\)表示

• 一个点初始在\(c_n\)处，逆时针做圆周运动，角速度是\(\omega=\frac{2\pi n}{T}\)，半径为\(c_n\)的模长
• 另一个点初始在\(c_{-n}\)处，顺时针做圆周运动，角速度是\(\omega=\frac{2\pi n}{T}\)，半径为\(c_{-n}\)的模长
• 两个点的圆周运动，看做向量（圆心与点连接）的转动，二者的加和就是向量的加和，\(f(t)\)就是加和后的向量随时间变化

考虑到\(c_n\)与\(c_{-n}\)共轭，因此模长相等，即它们运动半径相同；初始位置关于实轴对称，又做反方向运动，因此二者的加和会将虚数部分抵消，所以加和后的向量可以用一个实数表示。实数部分其实就是考虑\(\cos\)，因此圆周运动过程中，记录下余弦值，画出余弦值与时间的关系，就得到了一个波。这里与上一节对应一下

• 因为是两个点的运动过程叠加，所以该频率下的振幅是模长的2倍
• 因为这里记录的是\(\cos\)，所以与上文使用的\(\sin\)相位有个加和为\(\frac{\pi}{2}\)的关系

每个\(n\)可以得到一个波，叠加后可得到\(f(t)\)。或者这样做：每个\(n\)下都有2个点，分别用向量表示，所有\(2n\)个向量相加；每个时间\(t\)下相加得到的总是一个在实轴上的向量，记录下这个向量的值就能勾勒出\(f(t)\)的曲线。向量相加的过程就像下面这张图，图片来自wiki，这张图中两个向量频率相同，频率不同的动图可以见马同学

其实仔细想一想，向量相加和大圆套小圆的过程其实是一样的，二者分别对应傅里叶级数复数形式与实数形式的圆周运动解释。

其实大圆套小圆不仅可以画波，而且可以画出许多复杂的图像，比如画辛普森。画波与画图像的区别在于，波是时间的函数，一个时间对应一个值；而图像是一个时间对应一个二维坐标，将画纸看做复平面的话，图像也可以是时间的函数，只不过函数值是复数，由实部和虚部两部分构成；更进一步，波其实是虚部为0，如果看做点在复平面内的运动，就是在实数轴上来回摆动，我们只是加了一个时间轴，它画出的结果才是波的形式。因此，任意给定一个图形，如何计算它是由什么样的圆、如何运动绘制而成呢？只要取一些点，写出\(f(t)\)的形式，然后用公式\((7 )\)计算\(c_n\)，再转化为相位和振幅即可；\(f(t)\)是一个周期函数，或者是一个定义在有限区间的非周期函数。用套圆画图可以在这个网站中体验，你绘制一个图形，它会自动为你转化为大圆套小圆的形式。

傅里叶变换

非周期函数

非周期函数可以看做周期为无穷大的函数，下面我们考虑傅里叶级数周期增大，直至无穷会发生什么。

首先回顾周期函数的傅里叶级数展开 \[ f(x)=\sum_{n=-\infty}^\infty c_n e^{i\frac{2n\pi x}{T}} \tag{6} \]

\[ c_n=\frac{1}{T} \int_{-\frac T2}^{\frac T2} f(t) e^{-i\frac{2n\pi t}{T}} \mathrm{d}t , \quad n=0, \pm 1, \pm 2, \cdots \tag{7} \]

式\((6)\)是时域下的表示，式\((7)\)是频域下的表示，傅里叶级数分解是时域向频域的转化；频域中以频率为自变量，此时频率取离散值，\(\frac{n}{T},n=0,1,2,\cdots\)。可以看到，随着周期\(T\)的增大，频率的取值逐渐密集，可以想象，当周期趋近于无穷，频率将取连续值，此时式\((6)\)将不再是求和而是积分，这就是非周期函数的情形。将非周期函数时域向频域的转化，就对应傅里叶变换，下面我们写出傅里叶变换相关公式 \[ \begin{align} \text{傅里叶逆变换：}\qquad&f(x)=\int_{-\infty}^\infty F(w)e^{iwx} \mathrm{d}w\tag{9}\\ \text{傅里叶变换：}\qquad&F(w)=\frac{1}{2\pi}\int_{-\infty}^\infty f(t)e^{-iwt}\mathrm{d}t\tag{10} \end{align} \] 注意如下几点

1. 公式形式

• 这里频域中自变量\(w\)是角频率，使用频率也可以，只不过公式会稍微有一点常数上的差异，如下所示

\[ \begin{align} \text{傅里叶逆变换：}\qquad&f(x)= \int_{-\infty}^\infty F(v)e^{i2\pi vx} \mathrm{d}v\tag{11}\\ \text{傅里叶变换：}\qquad&F(v)=\int_{-\infty}^\infty f(t)e^{-i2\pi vt}\mathrm{d}t\tag{12} \end{align} \]

• 有一些版本的常数会和这里有些出入，如下所示

\[ \begin{align} \text{傅里叶逆变换：}\qquad&f(x)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty F(w)e^{iwx} \mathrm{d}w\\ \text{傅里叶变换：}\qquad&F(w)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty f(t)e^{-iwt}\mathrm{d}t \end{align} \]

对比后会发现如果给定\(f(t)\)，按照上面不同公式进行傅里叶变换，\(F(w)\)的结果不一致，差一个常数项；这不影响本质，因为傅里叶变换与逆变换公式是成对出现的，变换后如果想通过逆变换还原原来的\(f(t)\)，必须使用相应的逆变换形式。

2. 离散与连续

从频域图像的角度，非周期函数的频域图像，并不是将周期函数的图像不断密集取点，最后变成连续。从公式来说，式\((10)\)并不是由式\((7)\)简单取极限就可以得到。周期函数对应离散谱，非周期函数对应连续谱，二者有本质的区别。这有点像离散随机变量的概率分布，与连续随机变量密度函数的区别。离散谱取离散值，看柱子高度；而连续谱取连续值，看区域面积，而对于每个具体的点，面积都是0。

下面举一个例子，将矩形波从周期变换到非周期，对比公式直接取极限，与傅里叶变换之间的区别。

先以简单的方波为例，\(f(x)\)周期为\(T\)，一个周期内的函数形式如下所示

\[ f(x)=\left\{ \begin{array}{cl} 1,& \quad -\frac{T}{4}\leq x\leq \frac{T}{4}\\ 0,& \quad \frac{T}{4} < x\leq \frac{3T}{4}\\ \end{array} \right. \]

由式\((7)\)可以计算出

\[ c_n=\frac12 \frac{\sin(n\pi/2)}{n\pi/2} \]

由于\(f(x)\)是偶函数，所以\(c_n\)的虚部为0。下面我们要将周期增大到无穷，注意，如果我们直接令\(T \rightarrow \infty\)，可以看到\(c_n\)的结果并没有发生改变，因为这样增大周期结果还是一个方波，一直都还是周期函数；方波就是一个周期中取\(1\)的部分占比为\(50\%\)。我们增加周期要只增加\(0\)的部分，这样不断增加下去的结果是，只有\([-\frac{T}{4},\frac{T}{4}]\)区间内取值为\(1\)，其他区间为\(0\)，这就是一个非周期函数。一个周期为\(kT\)的函数定义如下 \[ f(x)=\left\{ \begin{array}{cl} 1,& \quad -\frac{T}{4}\leq x\leq \frac{T}{4}\\ 0,& \quad \frac{T}{4} < x\leq \frac{3T}{4}+(k-1)T\\ \end{array} \right. \] 由式\((7)\)可以计算出 \[ c_n=\frac{1}{2k} \frac{\sin(\frac{n\pi}{2k})}{\frac{n\pi}{2k}}=\frac{1}{2k} \mathrm{sinc}(\frac{n}{2k}) \] 已知\(x\rightarrow 0\)时，\(\mathrm{sinc}(x)\rightarrow 1\)，因此随着\(k\)的不断增大，柱子高度整体是逐渐减小的，当\(k\rightarrow \infty\)，柱子高度将趋近于0。下面这张图展示了随着周期不断增大，\(c_n\)随频率变化的图像

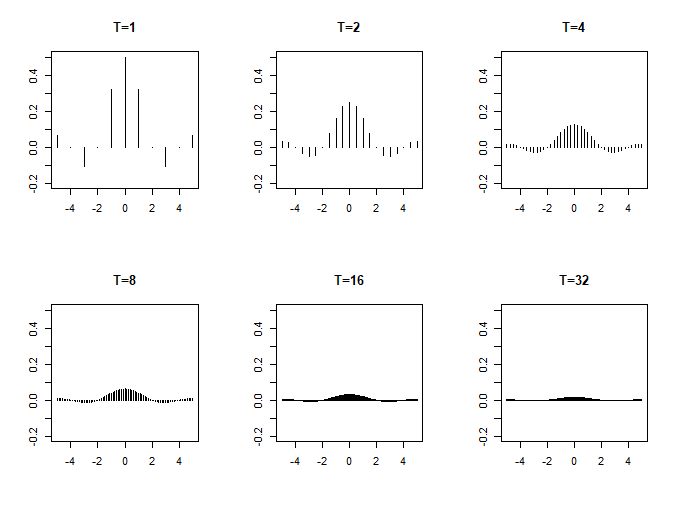
这种趋于0的效果，就像离散随机变量，随着定义域的扩大，可取的点原来越多，但每个点的取到的概率也会越来越小，取值为连续区间时，具体每个点的概率都为0；此时衡量单个点的概率就没有意义了，需要衡量的是区间的概率，画图也不画概率分布图了，而是画概率密度图。上面的离散谱（又称线谱）与概率分布类似，而傅里叶变换对应的连续谱（又称密度频谱）与概率密度类似。

对于只有\([-\frac{T}{4},\frac{T}{4}]\)区间内取值为\(1\)，其他区间为\(0\)的非周期函数，我们可以由式\((12)\)推导出频域下的密度表达 \[ F(v)=\frac{T}{2} \mathrm{sinc}(\frac{vT}{2}) \]

傅里叶变换后的结果一般是虚数，这里因为\(f(x)\)是偶函数，所以虚部为0。

3. 由傅里叶级数到傅里叶变换的推导

从式\((6,7)\)出发，将\(c_n\)形式带入式\((6)\)，对周期取极限得 \[ \begin{align} f(x)&=\lim_{T\rightarrow\infty} \sum_{n=-\infty}^\infty \left[\frac{1}{T} \int_{-\frac T2}^{\frac T2} f(t) e^{-i\frac{2n\pi t}{T}} \mathrm{d}t\right] e^{i\frac{2n\pi x}{T}} \\ &=\lim_{T\rightarrow\infty} \sum_{n=-\infty}^\infty \left[\frac{1}{T} \int_{-\frac T2}^{\frac T2} f(t) e^{i\frac{2n\pi }{T}(x-t)} \mathrm{d}t\right] \end{align} \] 令\(w_n=\frac{2n\pi}{T}\)，则\(\Delta w=w_n-w_{n-1}=\frac{2\pi}{T}\) \[ \begin{align} f(x)&=\lim_{T\rightarrow\infty} \sum_{n=-\infty}^\infty \left[\frac{1}{2\pi}\Delta w \int_{-\frac T2}^{\frac T2} f(t) e^{iw_n(x-t)} \mathrm{d}t\right] \\ &=\lim_{T\rightarrow\infty} \sum_{n=-\infty}^\infty \left[\frac{1}{2\pi} \int_{-\infty}^{\infty} f(t) e^{iw_n(x-t)} \mathrm{d}t\right]\Delta w \end{align} \] 当\(T\rightarrow\infty\)，\(\Delta w \rightarrow 0\)，所以有 \[ \begin{align} f(x)&=\int_{-\infty}^\infty \left[\frac{1}{2\pi} \int_{-\infty}^{\infty} f(t) e^{iw(x-t)} \mathrm{d}t\right]\mathrm{d} w \\ &=\int_{-\infty}^\infty \left[\frac{1}{2\pi} \int_{-\infty}^{\infty} f(t) e^{-iwt} \mathrm{d}t\right] e^{iwx}\mathrm{d} w \end{align} \] 令\(F(w)=\frac{1}{2\pi}\int_{-\infty}^\infty f(t)e^{-iwt}\mathrm{d}t\)，则有 \[ f(x)=\int_{-\infty}^\infty F(w)e^{iwx} \mathrm{d}w \]

周期函数

将傅里叶变换扩展到周期函数，则统一了周期函数与非周期函数的变换方式，之后傅里叶变换的性质可以对任意函数都成立。周期函数的频谱是离散的，只在特定的一些频率点不为0；而傅里叶变换是在求频谱密度，关注的是面积；所以需要定义一个冲激函数\(\delta(x)\)，定义如下

\[ \delta(x)=0, t\neq 0\\ \int_{-\infty}^{\infty} \delta(x)\mathrm{d}x = 1 \]

周期函数的傅里叶变换就是多个冲激函数的加和（其实就是将离散的位置变成冲激函数）。公式如下所示，其中\(f(x)\)是一个周期函数

\[ F(v)=\sum_{-\infty}^{\infty} c_n \delta(v-nv_0) \]

其中\(c_n=\frac{1}{T} \int_{-\frac T2}^{\frac T2} f(t) e^{-i2n\pi v_0 t } \mathrm{d}t, \quad n=0, \pm 1, \pm 2, \cdots\)，\(v_0=\frac{1}{T}\)。

上面公式的推导只是将式\((6)\)带入式\((12)\)，然后利用冲激函数的一个计算性质 \[ \int_{-\infty}^{\infty} e^{-i2\pi t(v-nv_0)}\mathrm{d}t =\delta(v-nv_0) \] 因为这个式子相当于对\(f(t)=e^{i2n\pi v_0t}\)做傅里叶变换，这是个周期函数，它的傅里叶级数展开就是在离散的\(nv_0\)处有\(c_n=1\)，用冲激函数表达相同的含义就如右式。所有周期函数用傅里叶级数展开都可以表示成\(f(t)=e^{i2n\pi v_0t}\)的加和，因此傅里叶变换都就是冲激函数的加和。

冲激函数的另一性质：任何函数与冲激函数做卷积，得到本身 \[ f(t)* \delta(t)=\int_{-\infty}^{+\infty} f(\tau) \delta(t-\tau) d \tau=f(t) \] 因为\(\delta(t-\tau)\)只有在\(\tau=t\)时不为0，所以 \[ \begin{align} f(t)* \delta(t)&=\int_{-\infty}^{+\infty} f(\tau) \delta(t-\tau) d \tau\\ &= f(t)\int_{-\infty}^{+\infty} \delta(t-\tau) d \tau\\ &=f(t) \end{align} \]

傅里叶变换的性质、离散傅里叶、应用、参考资料请见下一篇。