奇怪的R方

引言

在多元线性回归模型中，通常使用\(R^2\)来衡量拟合优度，其公式如下

\[R^2 = \frac{\sum_i(\hat y - \bar y)^2}{\sum_i(y_i-\bar y)^2} = 1-\frac{\sum_i (y_i - \hat y_i)^2 }{\sum_i (y_i - \bar y)^2}\]

线性回归是要找一条直线拟合当前数据，从第二个公式可以看出，如果我们把\(Y = \bar y\)这条水平线看成拟合数据最简单的模型，\(R^2\)的本质是当前模型比\(Y = \bar y\)模型好多少的度量。

从这个角度来看，使用一条带有截距项的直线拟合，一定比用不带截距项的直线拟合效果要好，因为后者是前者的一种特例（截距项为0），但是下面这个R语言中的例子的结果，却与这个认知相悖

1
2
3
4
5
6
7
8
9
10
11
# 设置随机种子，保证下面随机结果可以重复
set.seed(1234) 

# 生成随机数
x <- rnorm(1000, mean = 2)
y <- 2 + x + 2 * rnorm(1000)

fit <- lm(y ~ x)        # 带有截距项的模型
fit0 <- lm(y ~ x + 0)   # 不带有截距项的模型
summary(fit)
summary(fit0)

结果如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# 带有截距项的模型
> summary(fit)

Call:
lm(formula = y ~ x)

Residuals:
   Min     1Q Median     3Q    Max 
-6.332 -1.288  0.029  1.307  6.137 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.80913    0.13748   13.16   <2e-16 ***
x            1.11143    0.06218   17.87   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.96 on 998 degrees of freedom
Multiple R-squared:  0.2425,	Adjusted R-squared:  0.2417 
F-statistic: 319.5 on 1 and 998 DF,  p-value: < 2.2e-16


# 不带有截距项的模型
> summary(fit0)

Call:
lm(formula = y ~ x + 0)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.3572 -0.9835  0.3875  1.7358  8.4604 

Coefficients:
  Estimate Std. Error t value Pr(>|t|)    
x  1.84181    0.03036   60.67   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.122 on 999 degrees of freedom
Multiple R-squared:  0.7865,	Adjusted R-squared:  0.7863 
F-statistic:  3681 on 1 and 999 DF,  p-value: < 2.2e-16

可以看到，第二个模型的Multiple R-squared比第一个模型大很多。

这是为什么呢？

公式相异

没有截距项的模型\(R^2\)反而更大的原因在于，当使用没有截距项的线性回归模型时，R语言内部会使用另外一个公式

\[R_0^2 = \frac{\sum_i \hat y_i^2}{\sum_i y_i^2}=1-\frac{\sum_i(y_i-\hat y_i)^2}{\sum_i y_i^2}\]

\(R_0^2\)相比于\(R^2\)，不同之处只是将\(\bar y\)设置为0。这里要注意一点，不是说没有截距项时，\(R^2\)就可以推导出\(R_0^2\)；而是二者就是两个不同的公式，两个模型在用不同的方法计算R方。

我们先用R语言来验证这一点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 定义计算R方和R0方两个公式的函数
get_r <- function(fit) 1-mean((y-fitted(fit))^2) / mean((y-mean(y))^2)
get_r0 <- function(fit) 1-mean((y-fitted(fit))^2) / mean(y^2)

# summary给出的结果
summary(fit)$r.squared    # 0.242476
summary(fit0)$r.squared   # 0.7865377

# 用R方的公式计算
get_r(fit)                # 0.242476
get_r(fit0)               # 0.1110403

# 用R0方的公式计算
get_r0(fit0)              # 0.7865377

可以看到，如果两个模型都用\(R^2\)的公式来算，不加截距项的模型结果和summary给出的不一样，而且用这个公式计算结果符合我们的预期（加截距项的模型\(R^2\)更大）。而使用\(R_0^2\)公式计算结果和summary结果相同，\(R^2\)提高了很多。

接下来我们考虑，一个没有截距项的模型在计算时，完全也可以用它本身的\(\bar y\)，况且它本身的\(\bar y\)也不是0，为什么这里要做这样的变化呢？

因为合理！一个没有截距项的线性模型其实是受到了一定的限制，该模型拟合的好不好，当然要放在同一个平台上，跟同样没有截距项（受到相同限制）的模型中最朴素的比。也就是要跟\(Y=0\)比，而不是和\(Y=\bar y\)比。

用图形表示如下

1
2
3
4
5
6
7
8
9
10
plot(x, y, pch = 16, cex = 0.5,
     xlim = c(-1, 6), ylim = c(-1, 15), 
     xlab = 'x', ylab = 'y')
abline(h = 0, col = 'blue', lty = 2)
abline(h = mean(y), col = 'red', lty = 2)
abline(v = 0, col = 'grey')
abline(fit, lwd = 2, col = 'red')
abline(fit0, lwd = 2, col = 'blue')
legend('topleft', c('fit', 'fit0'), 
       lty = 1, col = c('red', 'blue'))

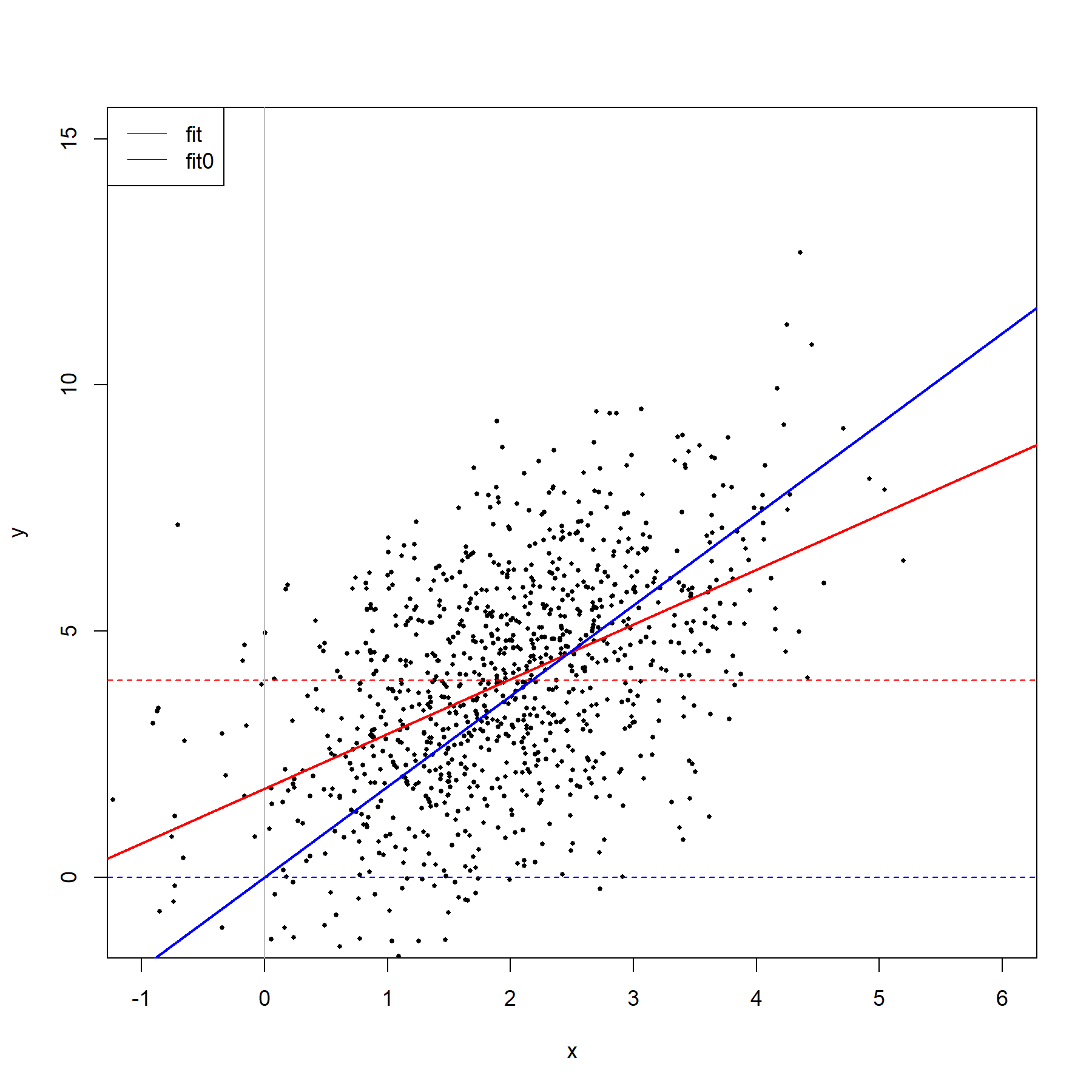
红色实线（带截距项模型）和红色虚线比，蓝色实线（不带截距项模型）和蓝色虚线比。

\(R^2\)为负

如果使用\(R^2\)的公式，没有截距项的模型有可能还没有\(Y=\bar y\)拟合的好，这就是\(R^2\)可能出现负数的一个原因；而和\(Y=0\)比则不会出现负数的情况。

下面首先用R语言给出一个\(R^2\)为负的例子

1
2
3
4
set.seed(1234)
x <- rnorm(100, sd = 2)
y <- 2 + 0.5 * x + rnorm(100)
fit0 <- lm(y ~ x + 0)

结果如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
> summary(fit0)

Call:
lm(formula = y ~ x + 0)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.7923  1.3491  1.9948  2.6062  4.7991 

Coefficients:
  Estimate Std. Error t value Pr(>|t|)   
x   0.3309     0.1122   2.949  0.00398 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.271 on 99 degrees of freedom
Multiple R-squared:  0.08073,	Adjusted R-squared:  0.07144 
F-statistic: 8.694 on 1 and 99 DF,  p-value: 0.003983

> get_r(fit0)
[1] -1.550429

下面我们从理论上简单说明一下，在没有截距项时，使用这个公式

\[R^2 = \frac{\sum_i(\hat y - \bar y)^2}{\sum_i(y_i-\bar y)^2} = 1-\frac{\sum_i (y_i - \hat y_i)^2 }{\sum_i (y_i - \bar y)^2}\]

时，\(R^2\)为负的原因。

这个公式还可以写成 \(R^2 = \frac{SSR}{SST}=1-\frac{SSE}{SST}\)，其中\(SST=SSE+SSR\)，即

\[\sum_i (y_i - \bar y)^2 = \sum_i (y_i - \hat y_i)^2 + \sum_i(\hat y_i-\bar y)^2\]

而这个式子要想成立，需要

\[\sum_i2(\hat y_i-\bar y)(y_i - \hat y_i)=0\]

因为\(SST\)是这样展开的

\[\sum_i (y_i - \bar y)^2 = \sum_i (y_i - \hat y_i)^2 + \sum_i(\hat y_i-\bar y)^2 + \sum_i2(\hat y_i-\bar y)(y_i - \hat y_i)\]

\[= \sum_i (y_i - \hat y_i)^2 + \sum_i(\hat y_i-\bar y)^2\]

在有截距项时，可以保证\(\sum_i2(\hat y_i-\bar y)(y_i - \hat y_i)=0\)（证明时需要用到在计算\(\hat \beta_{OLS}\)时，一阶导为0的条件）；而在没有截距项时，就无法保证其为0，也就无法保证\(SST>SSE\)，进而无法保证\(R^2>0\).